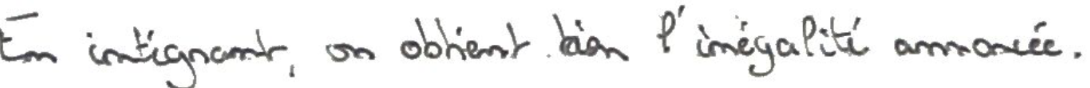Démontrer :

On a une première inégalité valable dans \({\Bbb R}_+\).
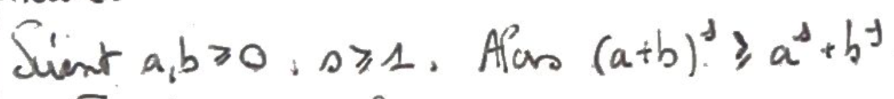
On peut l'appliquer en tout point pour se ramener à des puissances \(2\) à l'intérieur de la parenthèse.
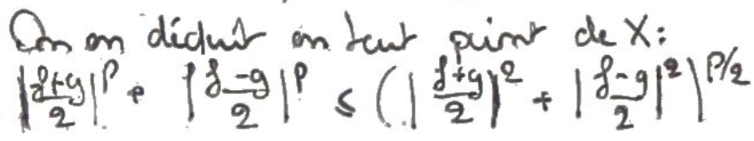
On peut maintenant appliquer l'Identité du parallélogramme.
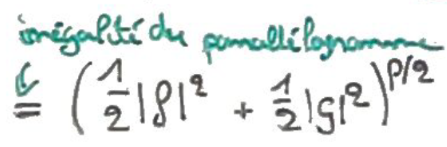
On applique ensuite la convexité de \(x\mapsto x^{p/2}\) (car \(p\geqslant 2\)).
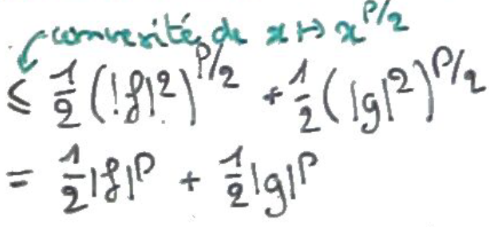
On conclut en intégrant.